"f(x)=x^r의 미분 공식에서 rx^(r-1) 이 된 과정에 대해 좀더 자세히 설명가능할까요?"
오늘 로봇 AI 회사에 면접을 다녀왔는데 면접 이후에, 이런 질문을 받았고 노션 페이지로 미분에 대해 기술한 다음 메일로
보내달라는 미션을 받았다. AI부트캠프를 수료했지만 아직도 미분에 대해 설명하지 못하는 내 자신을 보고 정말 한참 부족하구나,
이래서 계속 면접에서 떨어졌구나 라는 생각이 들어 깊게 공부를 해야겠다고 다짐했다.
그래서 미분을 아주 쉽게 이해할 수 있도록 내 스타일로 정리를 해보았고 메일로 보낸 미분 내용 정리를 다른 사람들도 볼 수 있도록 공유해 보기로 기쁜 마음을 먹었다. 나처럼 수학이 어려운 사람에게 미분에 대한 개념이 쉽게 자리 잡혔으면 좋겠다!
미분이란?
1. 미분의 정의
미분이란 한 점에서의 기울기를 뜻한다.
예를들어 A 와 B 점 사이의 기울기를 구하려면
기울기 = y증가량 / x증가량
의 식을 대입하여 예를들어
A(a, f(a)) 이고
B(a+h , f(a)+h)) 라면
기울기 = f(a+h) - f(a) / (a+h)-a
가 되는 것 이다.
그리고 미분은 x증가량이 거의 0 으로 갈 때의 기울기 이다.
x 증가량 = (a+h)-a = h
이기 때문에 h → 0 으로 보내는 과정이다.
따라서 미분식을 이렇게 표현할 수 있게 된다.
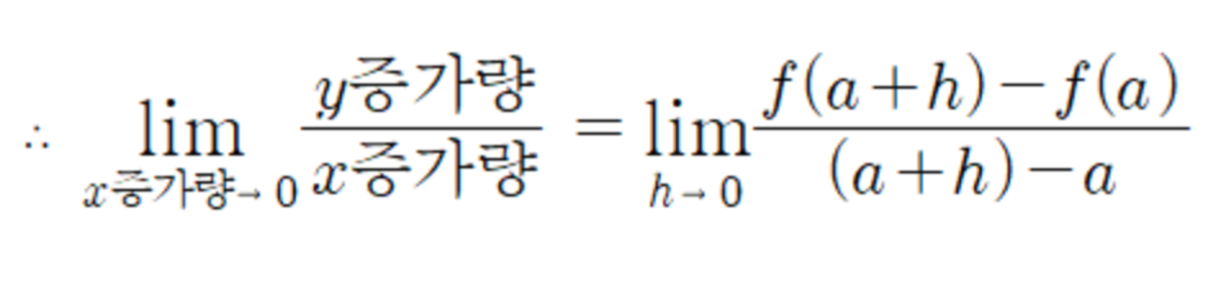
따라서 B점이 A점에 한없이 가까워 지게 되고, 그 동안에 기울기가 계속 변화할 것 이다.
결국 B점과 A점이 겹치게 되면서 A라는 한 점에서의 기울기를 알 수 있게 된다.
따라서 정리를 해보면
A(a, f(a)) 와 B(a+h), f(a+h)
사이의 기울기를 식으로 표현 한 후,
x증가량인 h 를 0 으로 보내버리면,
a 라는 한 점에서의 접선의 기울기가 된다.
2. 미분 하는 법
f(x) = x^r
(d/dx)x^r = r(x^(r-1)
f'(x) = r(x^(r-1)
유리함수 미지수 x의 미지수 r 승을 갖는 f(x) 에서 d/dx 는 x로 미분한다를 나타냄.
미분을 한 번 한 함수에는 ‘ 를 붙여 f’(x) 로 나타낸다.
x를 미분 할 경우, 우변과 같이 함수의 승수가 계수로 내려오며
승수에서 1을 빼준 값이 x의 승수가 된다.
만약 미지수가 r이 1 이라면 승수는 0 이 되고 미분한 값 f’(x) = 1 이 된다.
- 만약 상수를 미분한다면 값은 0 이 된다.
예시)
f(x) = x^2 → 미분 → f’(x) = 2x
3. 편미분이란?
편미분은 기본적으로 변수가 하나 이상인 다변수 함수를 대상으로 한다.
변수 x,y 가 있다고 할 때 하나의 변수를 미분하고
**남은 한 변수를 상수 취급**하는 것을 편미분이라고 한다.
f(x, y) = 2x+3xy + y^3에서 변수 x에 대하여 편미분하면 아래와 같다.
2 +3y
f(x, y) = 2x+3xy + y^3에서 변수 y에 대하여 편미분하면 아래와 같다.
3x + 3y^2
----------------------------------------------------------------------------------------------------------------------
함수 𝑓(𝑥)=𝑥𝑟의 미분 과정을 자세히 설명하겠습니다.
이 과정을 이해하려면 기본적인 미적분학 개념을 사용해야 합니다.
미분의 정의를 활용하여 𝑓(𝑥)를 미분하는 과정을 단계별로 살펴보겠습니다.
먼저, 𝑓(𝑥)=𝑥𝑟의 미분을 정의에 따라 계산해보겠습니다.
미분의 정의에 따르면,
𝑓′(𝑥)=limℎ→0𝑓(𝑥+ℎ)−𝑓(𝑥)ℎ입니다. 이제 이 정의를 𝑓(𝑥)=𝑥𝑟에 적용해보겠습니다.
1. 함수값 대입
𝑓(𝑥+ℎ)=(𝑥+ℎ)𝑟 𝑓(𝑥)=𝑥𝑟
2.정의에 대입
𝑓′(𝑥)=limℎ→0(𝑥+ℎ)𝑟−𝑥𝑟ℎ
3. 이항 전개 (Binomial Expansion)
𝑥+ℎ)𝑟를 전개하면 다음과 같이 표현할 수 있습니다:
(𝑥+ℎ)𝑟=𝑥𝑟+𝑟𝑥𝑟−1ℎ+𝑟(𝑟−1)2𝑥𝑟−2ℎ2+⋯+ℎ𝑟
4. 함수 차이 계산
(𝑥+ℎ)𝑟−𝑥𝑟=(𝑥𝑟+𝑟𝑥𝑟−1ℎ+𝑟(𝑟−1)2𝑥𝑟−2ℎ2+⋯+ℎ𝑟)−𝑥𝑟 =𝑟𝑥𝑟−1ℎ+𝑟(𝑟−1)2𝑥𝑟−2ℎ2+⋯+ℎ𝑟
5. 정의에 대입
𝑓′(𝑥)=limℎ→0𝑟𝑥𝑟−1ℎ+𝑟(𝑟−1)2𝑥𝑟−2ℎ2+⋯+ℎ𝑟ℎ
6.h로 나누기
𝑓′(𝑥)=limℎ→0(𝑟𝑥𝑟−1+𝑟(𝑟−1)2𝑥𝑟−2ℎ+⋯+ℎ𝑟−1)
7.극한 계산
𝑓′(𝑥)=𝑟𝑥𝑟−1여기서 ℎ가 0으로 갈 때, ℎ에 대한 항들은 모두 0이 됩니다.
따라서, 결과적으로, 𝑓(𝑥)=𝑥𝑟의 미분은 𝑓′(𝑥)=𝑟𝑥𝑟−1가 됩니다.
이 과정은 𝑟이 실수인 경우에도 성립하며, 자연수 𝑟에 대해서는 특히 쉽게 이해할 수 있습니다.
위 과정을 통해서 𝑥𝑟의 미분이 어떻게 𝑟𝑥𝑟−1가 되는지 이해할 수 있습니다.
'코드스테이츠' 카테고리의 다른 글
| SQL 서브쿼리 어디에 넣을지 쉽게 판단 하는 방법!! (2) | 2024.06.11 |
|---|---|
| Selenium 다운로드 및 설치 방법 종합 가이드 (0) | 2024.05.19 |
| [코드스테이츠] [week4] 1일차_advanced_과제 (0) | 2022.11.16 |
| [코드스테이츠] [week3] 2일차_advanced_과제 (0) | 2022.11.13 |
| [코드스테이츠] # [week3] 4일차_basic_과제 (0) | 2022.11.12 |

