Logistic Regression 은 회귀가 아닌 분류모델이다.
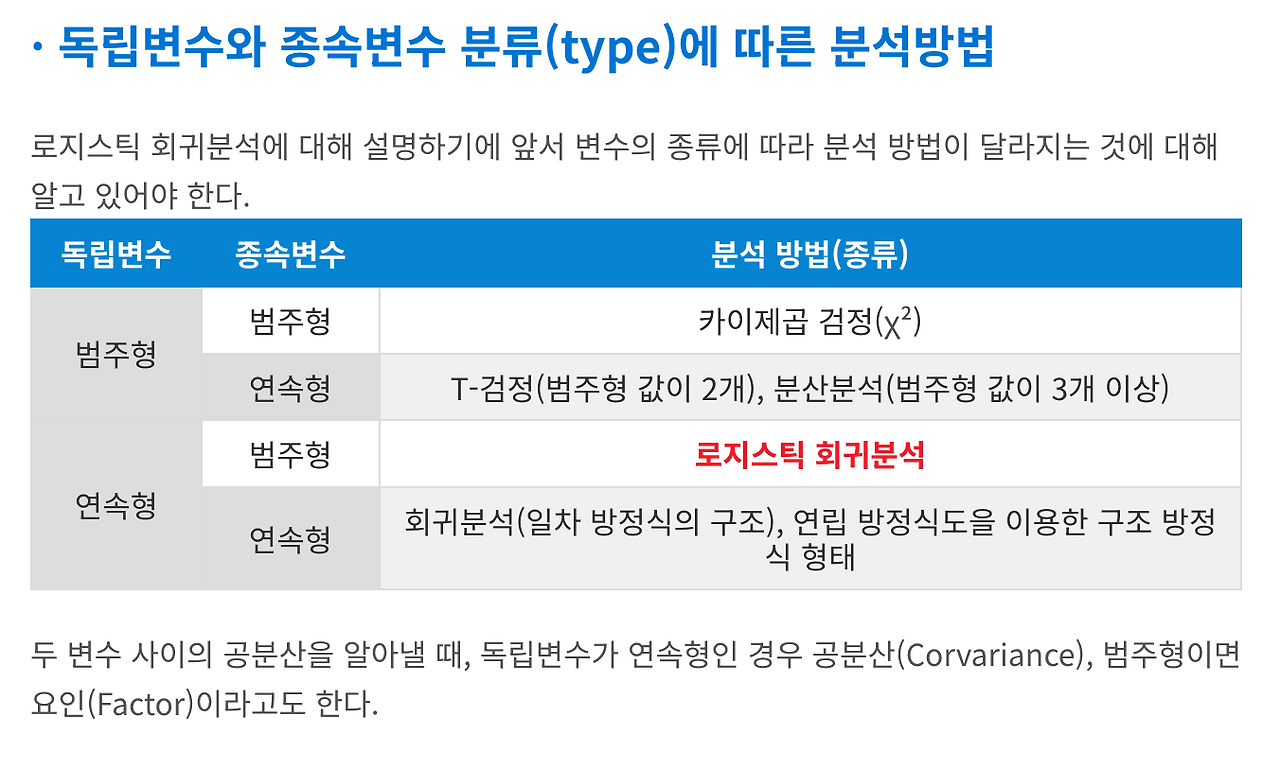
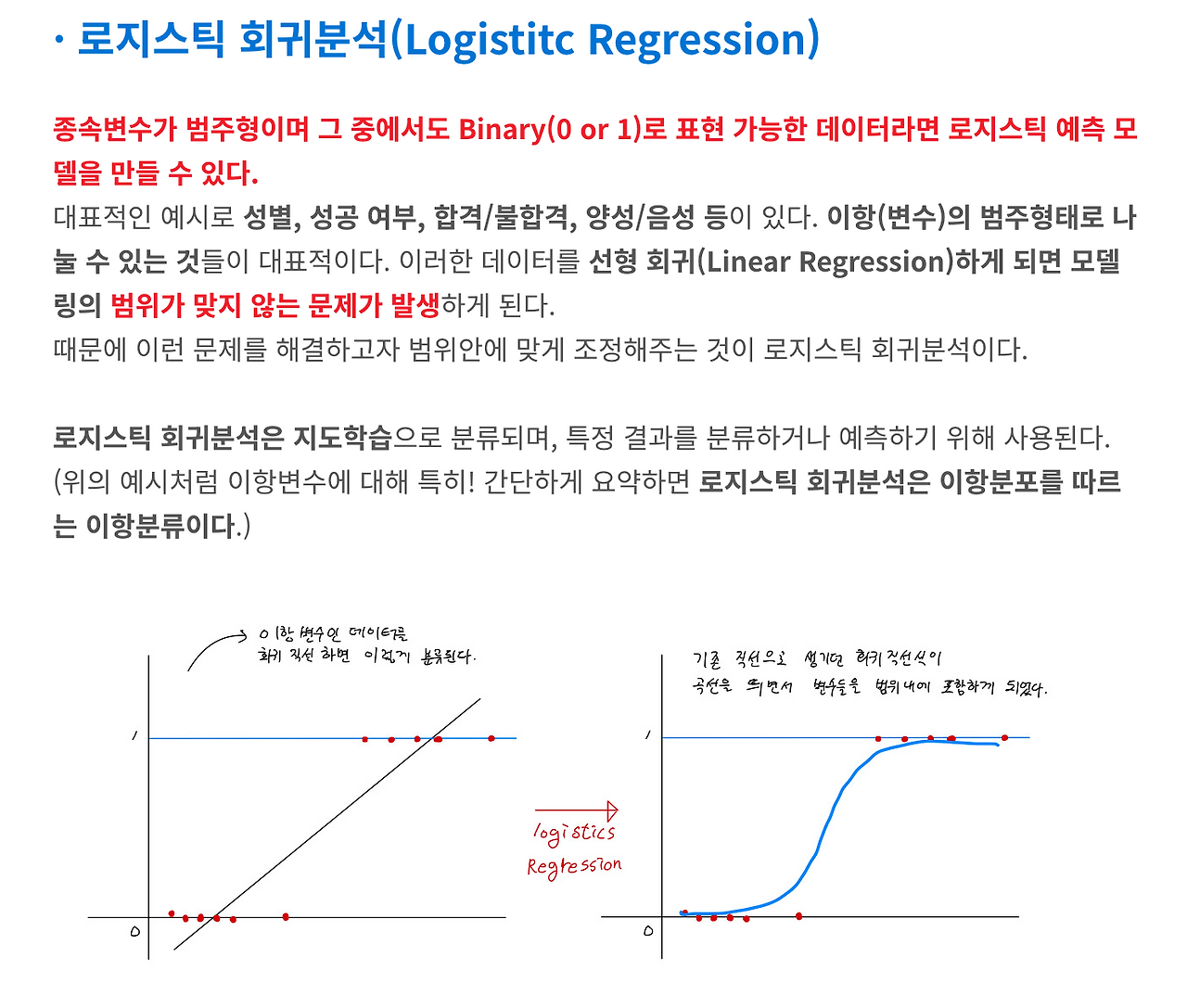
간단히 직접 그려서 알아보자!
import numpy as np
z = np.arange(-10, 10, 0.01)
g = 1 / (1+np.exp(-z))
import matplotlib.pyplot as plt
plt.plot(z, g)
plt.grid()
plt.show()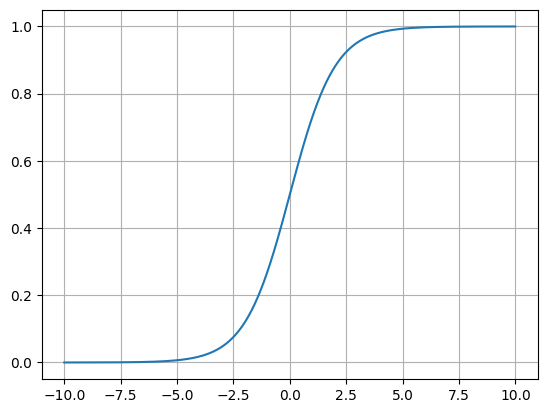
0,0.5를 딱 지나가는 그래프가 그려진다.
시그모이드 함수도 그려보자
plt.figure(figsize=(12,8))
ax = plt.gca() #설정값 변경 가능
ax.plot(z,g)
ax.spines['left'].set_position('zero')
ax.spines['bottom'].set_position('center')
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
plt.show()
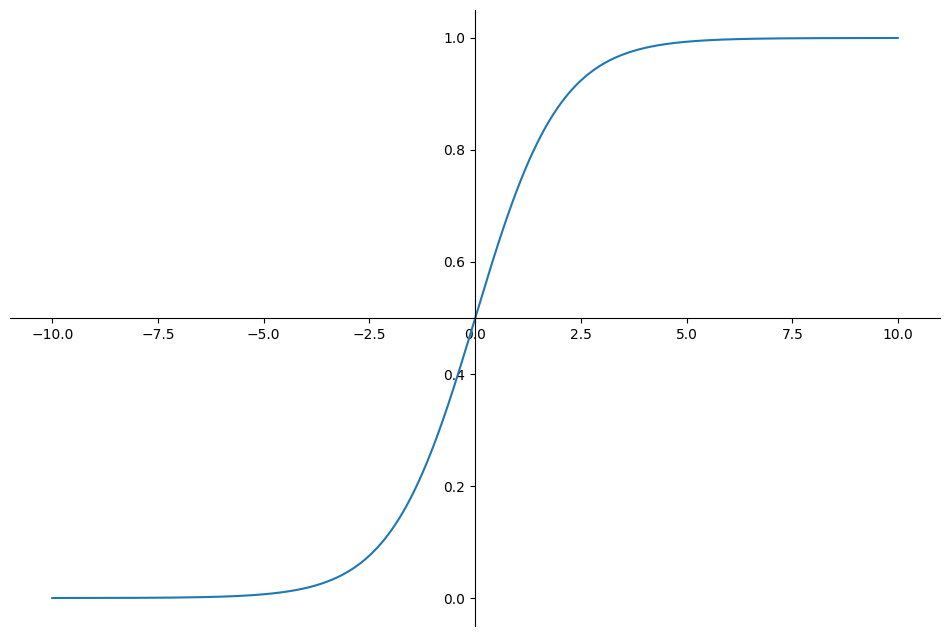
시그모이드는 아무리 작아도 0이고 아무리 커도 1이 나오는 함수이다.
Hypothesis 함수의 결과에 따른 분류
체크! h\theta(x) 는 주어진 입력 x(종양의 크기) 에서의 예측 결과가 1(악성) 이 될 확률을 의미함
-> h\theta(x) 가 0.7 이라면...환자의 종양이 악성일 확률이 70% 임.
따라서 0.5 보다 크면 1(악성), 작으면 0(양성) 이라고 분류를 해볼 수 있음.
+추가
Decision Boundary (결정경계)

Cost Function 을 재정의 (비용함수)
h = np.arange(0.01, 1, 0.01)
C0 = -np.log(1-h)
C1 = -np.log(h)
plt.figure(figsize=(12,8))
plt.plot(h, C0, label='y=0')
plt.plot(h, C1, label='y=1')
plt.show()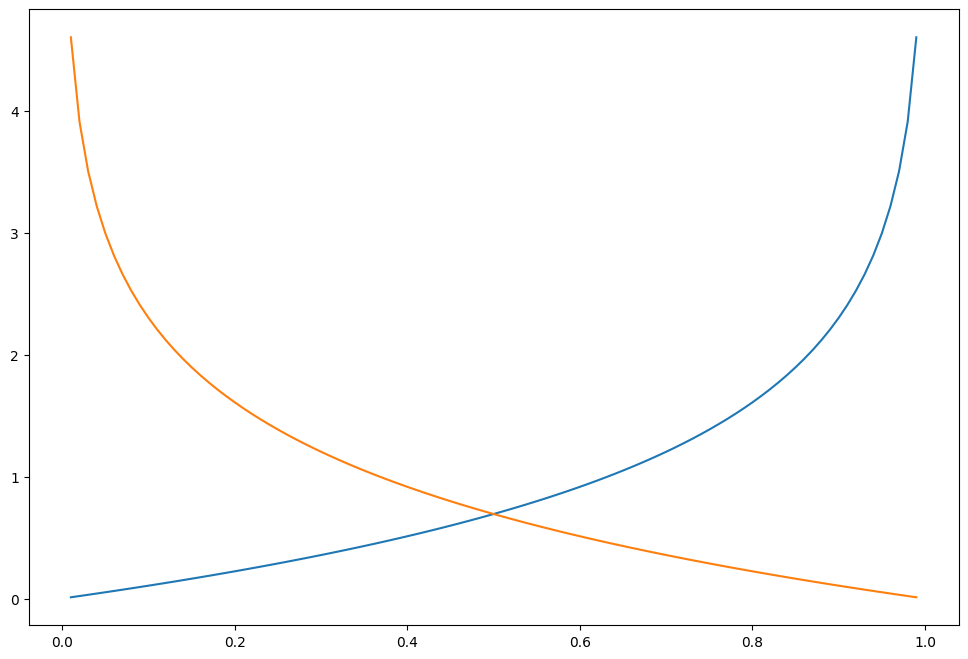
로지스틱 회귀는 시그모이드 함수에 직선을 넣어서 표현하는 함수이다.
다음에는 간단한 실습을 진행해볼 예정이다.

'ML.DL' 카테고리의 다른 글
| Min-Max-Scaler (1) | 2025.01.13 |
|---|---|
| Basic of Regression -OLS (1) | 2025.01.13 |
| 정밀도와 재현율 (1) | 2025.01.13 |
| 앙상블 기법 (1) | 2025.01.13 |
| Boosting Algorithm (0) | 2025.01.13 |



